| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Quadratic Probing
- singly linked list
- 노드 레벨
- 이진 큐
- Open-Addressing
- 루트노드
- array
- Queue
- 향상된 for문
- Gargbae Collector
- 배열
- 조상 노드
- 큐
- 직접 주소 개방
- 트리 높이
- 자바
- 부모 노드
- 해시 테이블
- Double Hasing
- binary queue
- 이차 조사법
- Double형 배열
- Linear Probing
- 선형 조사법
- 자료구조
- java
- 객체 배열
- 자식 노드
- ListIterator
- 단말노드
- Today
- Total
영운's 블로그
[자료구조 Java] 해시 테이블 (1) - 해시 테이블 및 해시 충돌(Hash Collision) 본문
[자료구조 Java] 해시 테이블 (1) - 해시 테이블 및 해시 충돌(Hash Collision)
[자료구조 Java] 해시 테이블 (3) - 시간 복잡도, 장점과 단점
[Java] 자바 Collection Framework의 HashMap은 어떤 해시 충돌 알고리즘을 사용할까?
key, 해시 함수, 해시 값 등 해시의 기본 개념을 살펴보고 이를 바탕으로 해시 테이블(Hash Table) 자료구조를 알아본다. 또한 해시 테이블에서 필연적으로 발생하는 해시 충돌(Hash Collision)에 대해서도 살펴보자.
해시 값(Hash Value), 해시 함수(Hash Function)이란?
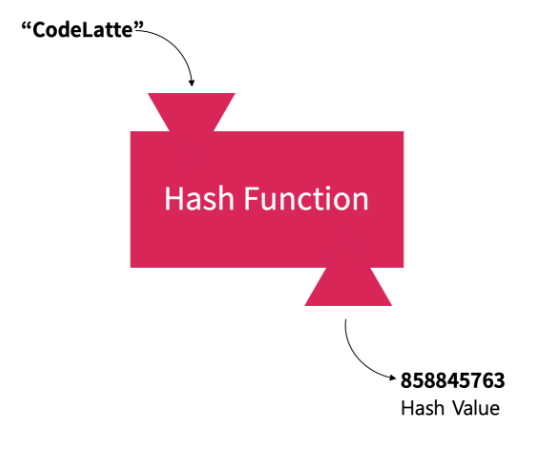
해시 테이블을 보기에 앞서 해시 값과 해시 함수에 대해 알야야 한다.
해시 함수는 key를 input으로 주면 output으로 해시 값을 도출한는 함수다.
해시함수의 input은 키(Key), output은 해시(Hash) 또는 해시 값(Hash Value)이라고 한다.
해시의 특징은 다음과 같다.
- 해시 함수는 동일한 key에 대해 output으로 언제나 동일한 해시 값을 도출한다.
- 해시 값과 해시 함수를 안다고 해도 input으로 들어온 키를 추측하기 어렵다.
- 값이 다른 key가 input으로 주어져도 동일한 output을 도출하는 '해시 충돌'이 발생할 가능성이 있다.
이러한 특징으로 해시는 암호화에 많이 사용되며 생각보다 실생활에서 많이 사용된다. 비밀번호를 해시 값으로 저장하면 해시 값이 해킹당해도 해시 값을 만든 실제 비밀번호는 유출되지 않기 때문이다.
기본적으로 대부분의 국가에서 사이트에서 회원의 비밀번호를 저장시 해시 값으로 저장하는 것이 의무이다. 만약 사이트 관리자가 회원들의 비밀번호를 알 수 있다면 이를 이용하여 다른 서비스에 접속을 시도하는 것이 가능하기 때문이다. 그렇기에 우리가 비밀번호를 잊어버려 비밀번호 찾기를 할 때 사이트에서 원래의 비밀번호가 아닌 이상한 문자를 대신 알려주는 것이다. 원래의 비밀번호는 서비스 관리자 본인도 알지 못하기 때문이다.
해시 테이블(Hash Table)이란?
해시 테이블은 key-value 구조로 데이터를 저장하는 자료구조로 키(Key)를 해시 함수(Hash Function)에 넣어 반환된 해시 값을 테이블의 인덱스로 사용한다.
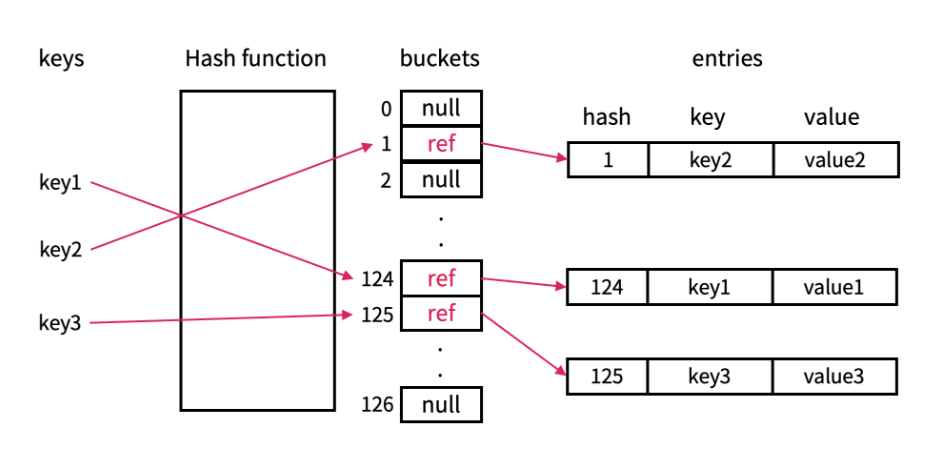
버킷(Bucket)과 엔트리('슬롯'이라 부르기도 함)는 해시 테이블의 저장소 역할로 버킷은 해시 값을 인덱스로 갖는 배열이며 엔트리의 주소를 저장하고 있다. 엔트리는 key-value에서 value인 실제 저장하고자 하는 데이터를 저장하고 있다.
해시 테이블은 탐색에 특화된 자료구조로 탐색에서 평균 O(1)의 시간복잡도를 갖는다는 장점을 갖는다. 단순히 key를 해시 함수에 넣어 index를 도출하고 그 값으로 테이블에 접근하면 되기에 해시 테이블은 빠른 탐색이 가능하다.
해시 충돌(Hash Collision)

해시 충돌이란 서로 다른 key값에 대해 동일한 해시 값이 도출하는 현상이다. 이는 해시 함수 자체의 문제보다는 해시 테이블 크기의 물리적 한계로 인한 경우가 많다. 이론적을 input으로 들어올 수 있는 key값은 무한하지만 해시 함수로 도출된 해시 값을 저장할 물리적 공간은 유한하다. 이를 거창하게 '비둘기 집의 원리'라고도 하는데 단순히 한 둥지에 한 마리의 비둘기가 들어가야 한다는 가정하에 n+1마리의 비둘기가 n개의 둥지에 들어가려 하면 한 비둘기는 둥지에 들어가지 못한다는 것이다.
해시에서는 비둘기 수(key로 들어올 수 있는 경우의 수)가 둥지의 수(버킷의 크기)보다 훨씬 더 많기에 해시 충돌은 필연적으로 발생하게 된다. 결국 이러한 해시 충돌을 최대한 줄이고 충돌 발생시의 처리방법이 해시 테이블의 성능을 결정한다. 이러한 해시 충돌 해결 방법은 Chaining과 Open-Addressing 이렇게 크게 2가지로 분류할 수 있다.
참고
https://www.codelatte.io/courses/java_data_structure
자바 자료구조 강의 - 코드라떼
컴퓨터 공학 2단계 자바 자료구조 강의입니다. 대부분의 프로그래밍하는 과정은 데이터를 다루는 일입니다. 데이터를 어떻게 잘 저장하고 관리할 수 있는지 자료구조에 대해 배웁니다. 자료구
www.codelatte.io
C언어로 쉽게 풀어쓴 자료구조 - 천인국, 공용해, 하상호
'자료구조' 카테고리의 다른 글
| [자료구조 Java] 해시 테이블 (3) - 시간 복잡도, 장점과 단점 (0) | 2022.07.17 |
|---|---|
| [자료구조 Java] 해시 테이블 (2) - 체이닝(Chaining), 선형 조사법(Linear Probing), 이차 조사법(Quadratic Probing), 이중 해싱법(Double Hasing) (0) | 2022.07.16 |
| [자료구조 Java] 힙(Heap), 이진 힙(Binary Heap) 개념 정리 + 자바로 구현하기 (1) | 2022.07.11 |
| [자료구조] 트리(Tree) 관련 용어 간단 정리 (0) | 2022.07.09 |
| [자료구조 Java] 이진 탐색 트리(Binary Search Tree) 개념 정리 + 자바로 구현하기 (0) | 2022.07.09 |