| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 큐
- singly linked list
- 자바
- Gargbae Collector
- Double Hasing
- 단말노드
- 배열
- Queue
- 향상된 for문
- 선형 조사법
- Double형 배열
- binary queue
- 조상 노드
- Linear Probing
- java
- 부모 노드
- 이진 큐
- 자식 노드
- 해시 테이블
- 이차 조사법
- 트리 높이
- 객체 배열
- Quadratic Probing
- Open-Addressing
- 루트노드
- 직접 주소 개방
- ListIterator
- 노드 레벨
- 자료구조
- array
- Today
- Total
영운's 블로그
[자료구조 Java] 이진 탐색 트리(Binary Search Tree) 개념 정리 + 자바로 구현하기 본문
이진 탐색 트리(Binary Search Tree) 필요성
탐색은 프로그램에서 가장 시간이 많이 걸리는 연산 중 하나이기에 효율적인 탐색을 구현하는 것은 굉장히 중요하다. 앞서 살펴본 스택, 큐, 배열, 리스트 구조는 모두 선형적인 구조를 갖고 있다. 선형적인 구조는 탐색 연산시 일일이 순차적으로 접근하여 데이터를 찾는 방식으로 탐색을 진행해야 하기에 탐색에 비효율적이다.
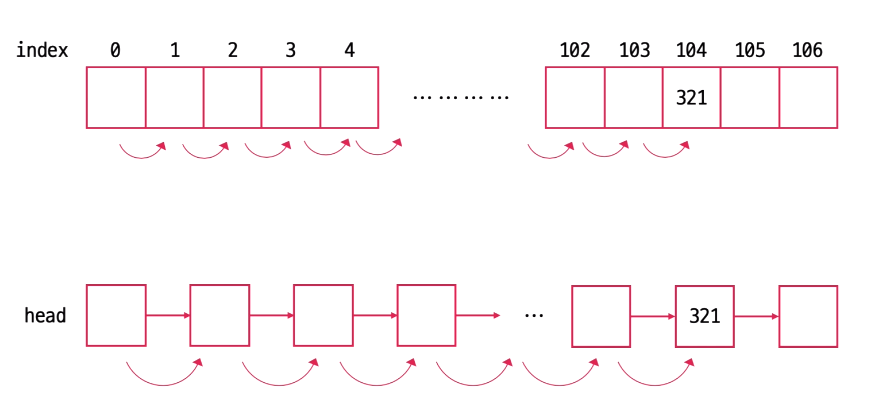
다음과 같이 배열과 연결리스트 모두 앞에서부터 순차적으로 탐색해야 값을 찾을 수 있고 최악의 경우 해당 값이 맨 마지막에 있다면 O(n)의 시간복잡도를 갖는다. 이러한 선형적인 구조의 탐색 비효율성은 데이터의 크기가 증가할수록 선형적으로 증가한다.
이러한 선형구조가 갖는 탐색의 비효율성을 개선한 것이 바로 이진 탐색 트리(Binary Search Tree)이다. 배열을 예시로 값이 100개 있는 경우 최고는 1번에 최악은 100번 탐색을 진행해 평균 50번 빅 오 표기법으로는 평균 O(N)의 시간 복잡도를 갖는다. 이진 탐색 트리는 술게임 중 하나인 up-down과 유사하다. 특정 값을 찾고자 한다면 루트 노드부터 시작해서 찾고자 하는 값이 더 크면 오른쪽 노드로 더 작으면 왼쪽 노드로 접근한다. 이진 탐색 트리는 노드가 100개 있는 경우 평균적으로 6~7번의 탐색을 거치며 빅 오 표기법으로 평균 O(logN) (밑이 2인)의 시간 복잡도를 갖는다.
이진 탐색 트리 전체 구조
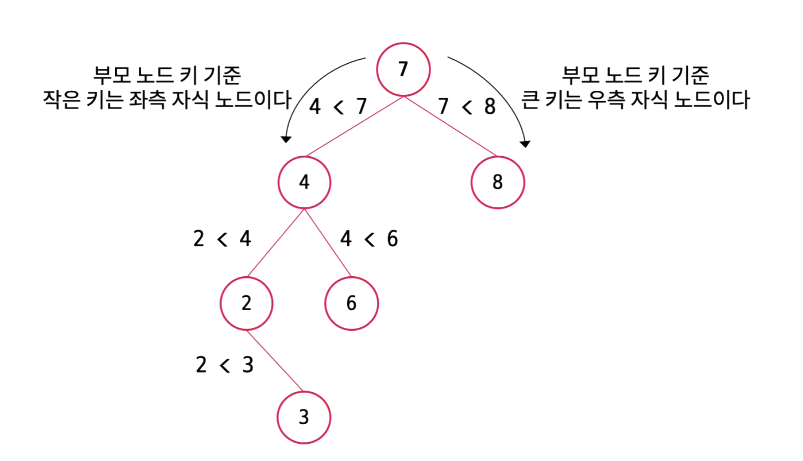
이진 탐색 트리는 계층적 구조를 갖는 이진 트리를 기반으로 한 자료구조로 부모 노드 기준 값이 작으면 왼쪽 노드로, 값이 크면 오른쪽 노드로 위치하는 트리이다. 하나의 노드는 값을 저장하는 key 변수와 자식 노드를 저장하는 left, right 참조 변수를 갖고 있다. 이진 탐색 트리는 언제라 '루트 노드'라는 높이가 0인 노드부터 접근하여 자식 노드들로 접근한다.
| 평균 | 최악 | |
| 검색 | O(log N) | O(N) |
| 삽입 | O(log N) | O(N) |
| 삭제 | O(log N) | O(N) |
이진 탐색 트리는 탐색에서 여전히 최악의 경우 O(n)의 시간복잡도를 갖지만 평균적으로 O(log2N)의 시간복잡도를 보인다.
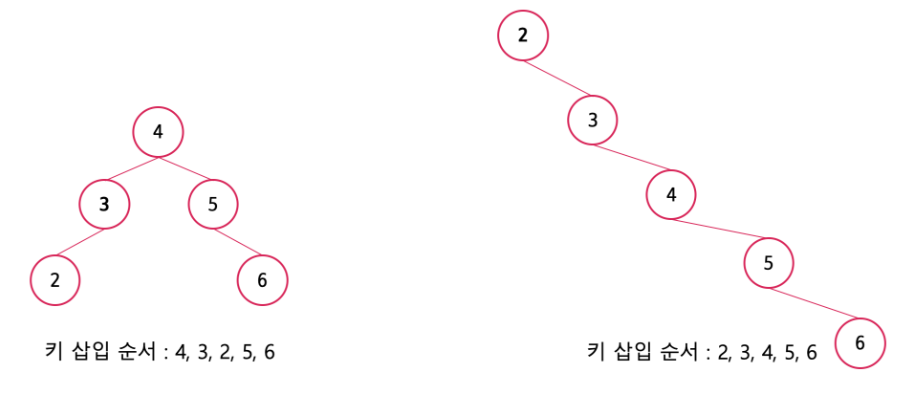
최악의 경우는 정렬된 값을 순서대로 삽입하는 경우이다. 이러한 경우 그림과 같이 리스트 형태가 되기에 이진 탐색 트리의 정의에는 부합하지만 사실상 선형적인 구조의 리스트 형태를 갖게 돼 이진 탐색 트리의 장점을 제대로 활용하지 못한다. 이처럼 이진 탐색 트리는 삽입 순서에 따라 형태가 달라진다는 단점을 가지고 있으며 이를 극복한 자료구조는 AVL 트리이다. AVL 트리는 삽입 순서에 상관 없이 균형을 유지하는 트리이다.
이진 탐색 트리의 핵심은 '탐색'이고, 탐색은 값이 있는지 없는지 찾는 것이기에 이진 탐색 트리는 중복값을 허용하지 않는다.
public class Node {
Node left = null;
Node right = null;
Integer key = null;
}
public class BinarySearchTree {
Node root = null;
...
}
트리 관련 용어 정리
트리라는 개념이 처음인 경우 해당 링크에서 트리에서 자주 사용되는 용어를 가볍게 살펴보는 것을 추천한다. 개념 자체가 어렵다기 보다는 용어가 생소하여 헷갈리는 것이 많기 때문이다.
이진 탐색 트리 삽입

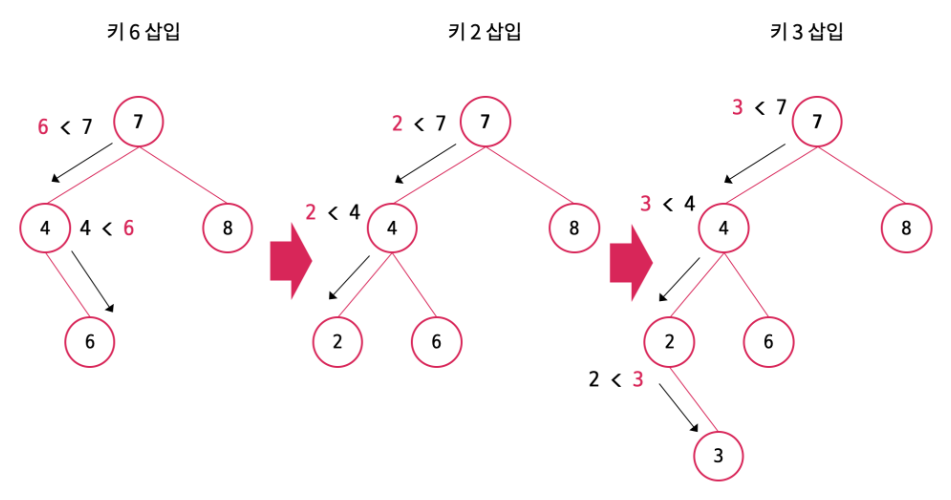
삽입 연산은 비교적 간단한다.
루트 노드가 존재하지 않는 처음 삽입인 경우 단순히 해당 노드를 루트 노드로 설정하면 된다.
루트 노드가 존재하는 경우 이진 탐색 트리의 규칙인 왼쪽 노드는 자신보다 작고 오른쪽 노드는 자신보다 크다는 특징을 이용하여 루트 노드부터 시작하여 삽입할 노드가 더 작으면 왼쪽 자식 노드로 보내고 더 크면 오른쪽 자식노드로 보낸다. 이를 더 이상의 이동이 필요 없을 때 까지 반복한다.
삽입 연산은 Node를 return하는 재귀적인 구조인데 마지막까지 반복한 경우 삽입할 노드를 return하고 그렇지 않은 경우 삽입할 노드와 비교한 노드를 return한다. 재귀적인 구조라 글로 쓰면 복잡해 보이지만 코드로 보면 그리 복잡하지는 않다.
재귀적 구조의 장단점은 다음과 같다
재귀적인 구조의 장점: 코드 구현이 간단하다는 것이다.
재귀적인 구조의 단점: 함수를 여러 번 호출하여 스택에 할당되기에 반복문으로 작성한 코드에 비해 성능이 떨어진다.
public void add(int key) {
Node newNode = new Node();
newNode.key = key;
if (root == null) {
root = newNode;
} else {
root = addNode(root, newNode);
}
}
private Node addNode(Node node, Node newNode) {
if (node == null)
return newNode;
else if (node.key > newNode.key)
node.left = addNode(node.left, newNode);
else
node.right = addNode(node.right, newNode);
return node;
}
이진 탐색 트리 삭제
경우1. Leaf node를 삭제
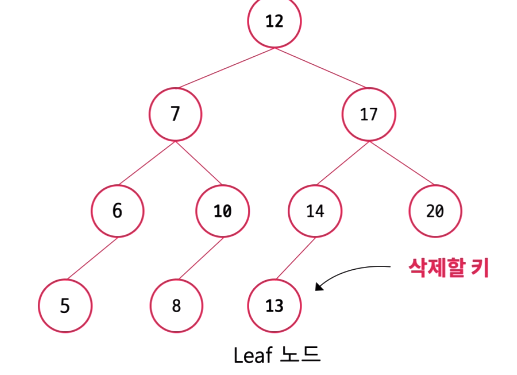
맨 밑에 있는 Leaf 노드를 삭제하는 것은 간단하다. 단순히 Leaf 노드의 부모 노드가 해당 Leaf 노드와의 연결을 끊어 주면 된다.
경우 2. 중간 노드를 삭제
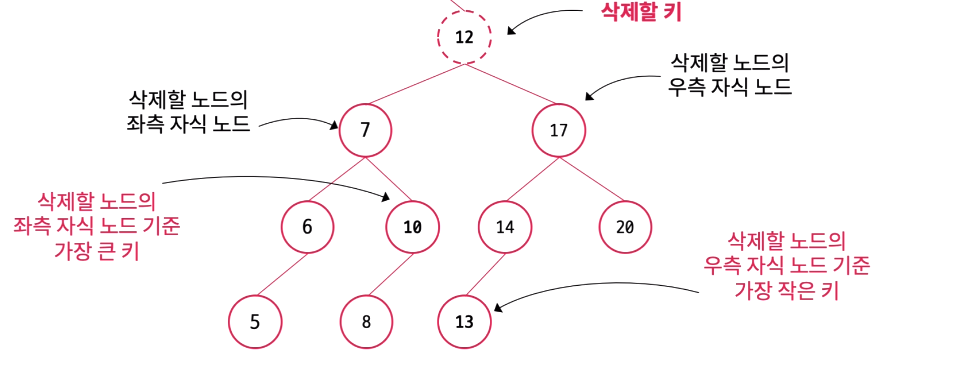
이진 탐색 트리 삭제의 핵심은 중간 노드를 삭제한는 경우이다. 단순히 중간 노드를 삭제한다면 전체적인 이진 탐색 트리의 구조가 무너지기 때문에 삭제할 노드를 대체할 노드를 찾아 이진 탐색 트리의 구조에 맞게 해당 위치로 옮겨야 한다. 실제 구현시에는 노드를 정말 옮기는 것은 아니고 단지 두 노드의 key값을 바꾼다.
key 값을 대체할 노드는 삭제한 노드의 키 기준 왼쪽 서브트리의 가장 오른쪽에 있는 노드 또는 오른쪽 서브트리의 가장 왼쪽에 있는 노드이다. 서브트리가 하나만 있으면 해당 서브트리에서 대체 노드를 찾으면 되며 두 개의 서브트리가 있다면 어느 쪽의 서브트리에서 대체 노드를 찾아도 무방하다.
잘 살펴보면
왼쪽 서브트리의 가장 오른쪽에 있는 노드 = 해당 서브트리에서 가장 큰 값
오른쪽 서브트리의 가장 왼쪽에 있는 노드 = 해당 서브트리에서 가장 작은 값
임을 알 수 있다.
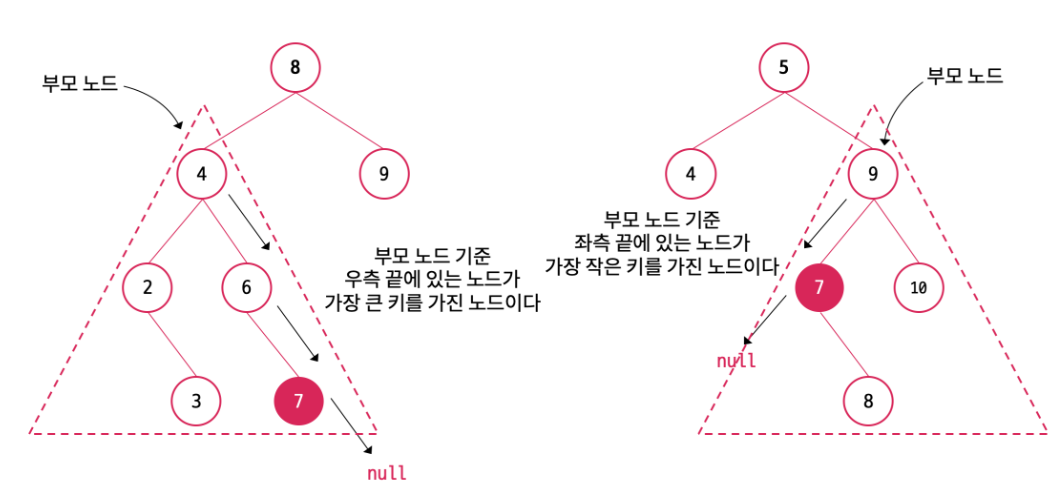
결국 해당 행동은 삭제한 노드 기준 가장 가까운 값을 키로 갖는 노드를 대체함으로써 노드의 이동을 최소화하면서 전체 이진 탐색 트리의 구조를 유지하는 것이다.
key값을 바꿔 삭제할 노드가 옮겨진 위치의 서브트리에 대해 삭제할 노드가 단말 노드가 될 때까지 재귀적으로 반복한다. 어떻게 보면 분할 정복(Divide and Conquer)에 해당되는데 위에서 살펴본 경우1. leaf node 삭제의 연산은 간단했다. 따라서 복잡한 경우2. 중간 노드를 삭제를 간단한 경우1.로 만들어 해결하는 것이다.
구체적인 삭제 방법은 다음과 같다. 그림은 왼쪽 서브트리의 가장 오른쪽에 있는 노드로 삭제할 노드를 대체하고 있다.
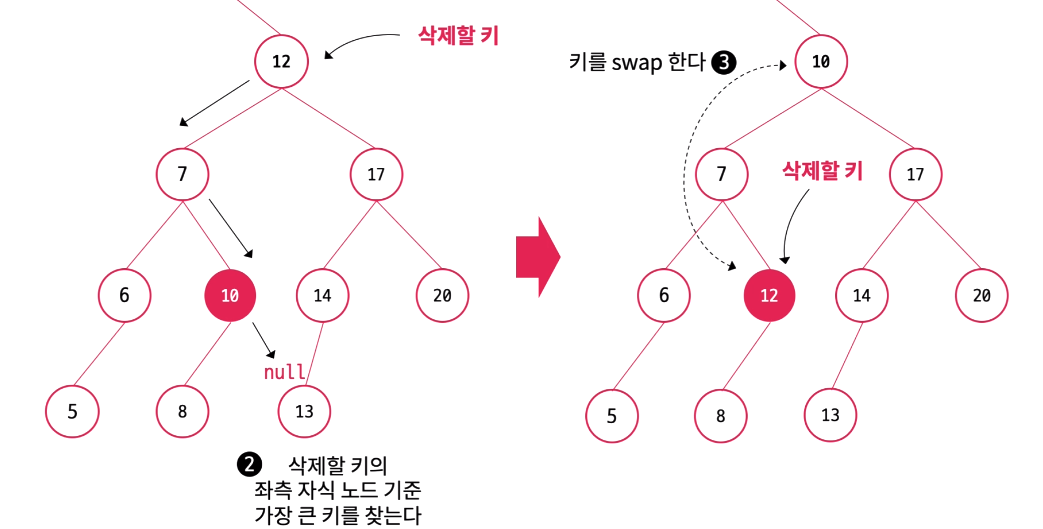

구체적인 구현 방법은 다음과 같다
- 삭제할 노드를 찾는다
- 삭제할 노드 기준 왼쪽(or 오른쪽) 서브트리의 가장 오른쪽에 있는 노드(=해당 서브트리에서 가장 큰 노드)를 찾는다.
- 삭제할 노드와 대체할 노드의 위치를 변경한다(key 값만 바꾼다. 그래야 두 노드와 연결된 다른 노드들과의 관계를 유지하기 때문)
- 위치가 변경된 삭제할 노드를 기준으로 삭제할 노드가 leaf node가 될 때까지 1~3을 반복한다.
- 삭제할 노드가 단말 노드(leaf node)가 되었다면 삭제할 노드의 부모 노드는 삭제할 노드와의 연결을 끊는다. (Java의 Garbage Collector가 더 이상 참조되니 않는 삭제할 노드의 메모리를 해제한다.)
public void remove(int key) {
root = removeNode(root, key);
}
private Node removeNode(Node node, int key) {
if (node == null)
throw new RuntimeException("해당 값을 가진 노드를 찾을 수 없습니다.");
if (node.key > key)
node.left = removeNode(node.left, key);
else if (node.key < key) {
node.right = removeNode(node.right, key);
} else {
//삭제할 노드를 찾은 경우
if (node.left != null) {
//왼쪽 서브트리에서 가장 오른쪽에 있는 값 찾아 대체하기
Node child = findMaxNode(node.left);
int removedKey = node.key;
node.key = child.key;
child.key = removedKey;
//다시 옮겨진 위치에서 서브트리에 대해 재귀적으로 실행
node.left = removeNode(node.left, key);
} else if (node.right != null) {
//오른족 서브트리에서 가장 왼쪽에 있는 값 찾아 대체하기
Node child = findMinNode(node.right);
int removedKey = node.key;
node.key = child.key;
child.key = removedKey;
//다시 옮겨진 위치에서 서브트리에 대해 재귀적으로 실행
node.right = removeNode(node.right, key);
} else {
//삭제할 노드가 단말 노드인 경우 부모 노드와의 연결 종료
return null;
}
}
return node;
}
private Node findMaxNode(Node node) {
if (node.right == null)
return node;
else
return findMaxNode(node.right);
}
private Node findMinNode(Node node) {
if (node.left == null)
return node;
else
return findMinNode(node.left);
}
이진 탐색 트리 순회 및 탐색
순회는 처음부터 끝까지 전체 노드에 접근하는 것이고 탐색은 순회를 하다 특정 값을 찾으면 순회를 멈추는 것이기에 결국 순회와 탐색은 동일한 논리 구조를 갖는다. 따라서 순회와 탐색을 별도로 구분하지 않고 같이 알아본다.
앞서 배운 스택, 큐, 배열, 리스트 등과 다르게 이진 탐색 트리의 탐색 방법은 여러가지다. 이진 탐색 트리가 선형적인 구조가 아니기에 여러가지 탐색이 가능한 것이다. 또한 그렇기 때문에 이진 탐색 트리에서 순차적인 탐색은 중요하다. 탐색을 하더라도 순차적인 탐색이 아닌 경우 비효율적인 탐색이 되기 때문이다.
이진 트리 순회에는 크게는 3가지 방법이 있으며 3가지 방법 모두 재귀적인 방법으로 구현된다.
1) 전위 순회(preorder traversal)
2) 중위 순회(inorder traversal)
3) 후위 순회(postorder traversal)
전위 순회는 1. 부모 노드 => 2. 왼쪽 서브트리 => 3.오른쪽 서브트리
중위 순회는 1. 왼쪽 서브트리 => 2. 부모 노드 => 3. 오른쪽 서브트리
후위 순회는 1. 왼쪽 서브트리 => 2. 오른족 서브트리 => 3. 부모 노드
순으로 순회하는 것을 의미한다.
전위 순회는 부모 노드를 먼저 처리하고 자식 노드를 처리해야 하는 경우,
후위 순회는 디렉토리의 용량을 계산하는 것처럼 자식 노드를 먼저 처리하고 부모 노드를 처리해야 하는 경우 사용된다. 중위 순회는 전위 순회와 후위 순회의 가운데에 위치한다.
3가지 순회 방법중 이진 탐색 트리의 순차적 탐색을 위한 순회에는 중위 순회가 가장 적절하다. 이는 이진 탐색 트리가 부모 노드 기준 왼쪽 자식 노드는 값이 작고 오른쪽 자식 노드는 값이 크다는 성질을 갖고 있기 때문이다.
중위 순회도 왼쪽 서브트리, 오른쪽 서브트리 중 어떤 트리를 먼저 순회할 것인가에 따라 좌측 중위 순회, 우측 중위 순회로 나뉜다. 좌측 중위 순회는 왼쪽 서브트리를 먼저, 우측 중위 순회는 오른쪽 서브트리를 먼저 탐색하는 중위 순회이다.
단순히 서브트리의 탐색 순서를 바꾼 것 같지만 이 탐색순서로 내림차순 탐색 혹은 오름차순 탐색이 결정된다.
좌측 중위 순회 => 오름차순 순회
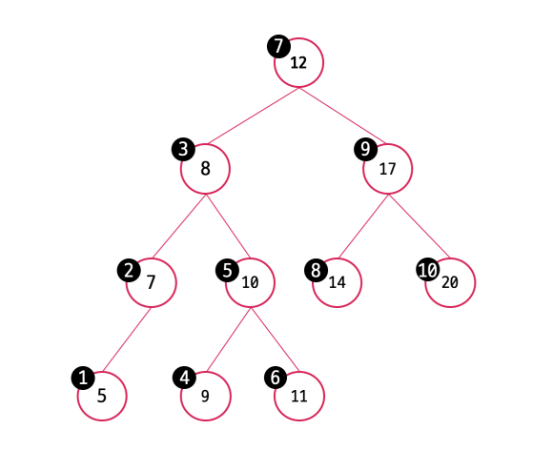
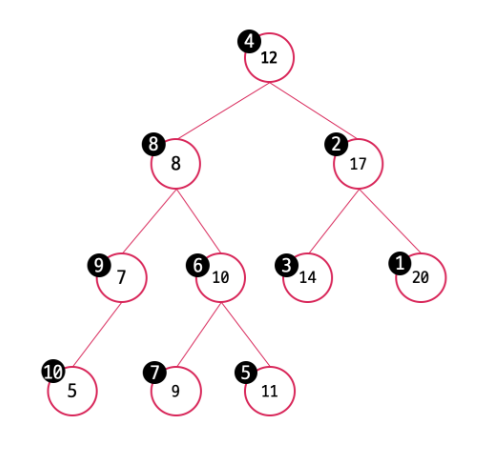
우측 중위 순회 => 내림차순7 순회
public void search(int key) {
searchNode(root, key);
}
private Node searchNode(Node node, int key) {
if (node == null)
throw new RuntimeException("해당 값을 가진 노드를 찾을 수 없습니다.");
if (node.key > key)
node.right = searchNode(node.right, key);
else if (node.key < key)
node.left = searchNode(node.left, key);
else
System.out.println("해당 값을 가진 노드를 찾았습니다.");
return node;
}
public void descendingTraversal() {
//내림차순 순회
System.out.print("내림차순 순회: ");
rightInorderTraversal(root);
System.out.println();
}
private void rightInorderTraversal(Node node){
//우측 중위 순회
if(node == null)
return;
rightInorderTraversal(node.right);
System.out.printf("%d ", node.key);
rightInorderTraversal(node.left);
}
public void ascendingTraversal() {
//오름차순 순회
System.out.print("오름차순 순회: ");
leftInorderTraversal(root);
System.out.println();
}
private void leftInorderTraversal(Node node) {
//좌측 중위 순회
if(node == null)
return;
leftInorderTraversal(node.left);
System.out.printf("%d ", node.key);
leftInorderTraversal(node.right);
}
코드 실행
public class Main {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
bst.add(12);
bst.add(8);
bst.add(7);
bst.add(5);
bst.add(10);
bst.add(9);
bst.add(11);
bst.add(17);
bst.add(14);
bst.add(20);
bst.ascendingTraversal();
bst.descendingTraversal();
System.out.println("key 12 갖는 노드 삭제");
bst.remove(12);
bst.ascendingTraversal();
bst.descendingTraversal();
bst.search(11);
//트리에 없는 key 찾으려 하여 오류 발생
// bst.search(12);
}
}
- 실행 결과 -

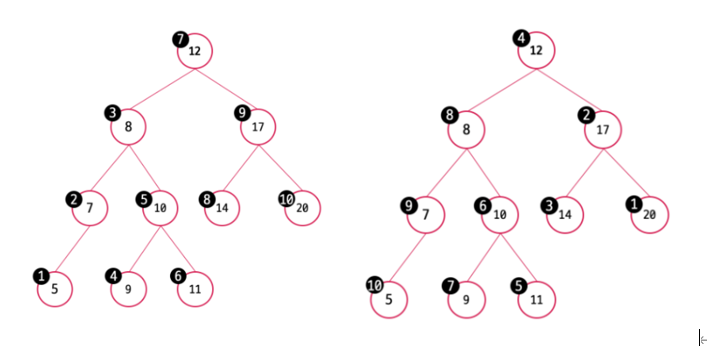
그림과 동일한 순서의 결과를 도출한다.
전체 코드
https://github.com/you88311/data-structure
GitHub - you88311/data-structure
Contribute to you88311/data-structure development by creating an account on GitHub.
github.com
참조
https://www.codelatte.io/courses/java_data_structure
자바 자료구조 강의 - 코드라떼
컴퓨터 공학 2단계 자바 자료구조 강의입니다. 대부분의 프로그래밍하는 과정은 데이터를 다루는 일입니다. 데이터를 어떻게 잘 저장하고 관리할 수 있는지 자료구조에 대해 배웁니다. 자료구
www.codelatte.io
C언어로 쉽게 풀어쓴 자료구조 - 천인국, 공용해, 하상호 지음
'자료구조' 카테고리의 다른 글
| [자료구조 Java] 힙(Heap), 이진 힙(Binary Heap) 개념 정리 + 자바로 구현하기 (1) | 2022.07.11 |
|---|---|
| [자료구조] 트리(Tree) 관련 용어 간단 정리 (0) | 2022.07.09 |
| [자료구조 Java] 큐(Queue) 개념 정리 + 자바로 구현하기 (0) | 2022.07.07 |
| [자료구조 Java] 스택(Stack) 개념 정리 + 자바로 구현하기 (0) | 2022.07.02 |
| [자료구조 Java] 이중 연결리스트(Doubly Linked List) 핵심 정리 (0) | 2022.07.01 |