| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 큐
- 이차 조사법
- 부모 노드
- 선형 조사법
- ListIterator
- Queue
- singly linked list
- 트리 높이
- 단말노드
- 직접 주소 개방
- Quadratic Probing
- java
- Gargbae Collector
- binary queue
- 이진 큐
- 노드 레벨
- 루트노드
- Linear Probing
- 자식 노드
- 배열
- 향상된 for문
- Double Hasing
- 해시 테이블
- Open-Addressing
- 조상 노드
- 객체 배열
- 자료구조
- Double형 배열
- array
- 자바
- Today
- Total
영운's 블로그
[자료구조 Java] 이중 연결리스트(Doubly Linked List) 핵심 정리 본문
이중 연결리스트(Doubly Linked List)의 개념을 정리하고 이를 자바(Java)로 구현하고자 한다. 마지막에는 자바의 Collction Framework에 있는 LinkedList 사용시 반복문 관련 주의할 점을 알아본다.
이중 연결리스트란?

이중 연결리스트는 '단일_연결리스트'와 비교하였을 때 노드가 양방향으로 연결되었다는 차이점을 갖는다. 단일 연결리스트에 있던 head변수와 추가적으로 마지막 노드를 가리키는 tail 변수를 갖는다. tail 변수가 추가됨에 따라 마지막 노드에서 역행적으로 선행 노드로의 접근이 가능해져 접근 연산이 훨씬 빨라진다. 단일 연결 리스트도 Tail 변수를 추가할 수 있지만 리스트의 마지막을 의미할 뿐 단일 연결이기에 리스트의 뒤에서부터 앞으로의 접근은 불가능하기에 단순히 null을 저장하여 리스트의 마지막을 저장하던 것과 대비된다.

하나의 노드는 다음과 같이 left, right, data 변수를 갖는다. left 변수에는 선행노드의 주소가 right 변수에는 후행노드의 주소가 저장된다. 맨 앞 노드의 left변수와 맨 뒤 노드의 right변수에는 null이 저장되어 해당 노드가 맨 앞 혹은 맨 뒤 노드임을 알 수 있다.
이중 연결리스트의 head와 tail변수를 구현하는 방법은 2가지이다.
1) 별도의 header노드를 만들어 left변수에 tail, right변수에 head를 저장하는 방법
2) 주소값을 가리키는 tail, head 객체를 선언하는 방법이다.
일반적으로 이중 연결리스트는 맨 앞 노드와 맨 뒤 노드가 연결된 원형 연결리스트의 특징까지 갖는 이중 원형 연결리스트를 만들어 사용한다. 방법1은 그 자체가 원형 연결리스트까지 갖는 다는 장점이 있다. 방법2의 경우에도 원형 연결리스트의 특징을 추가할 수 있지만 별도로 left변수나 right변수가 null인지 확인하는 추가적인 구현이 필요하다. 하지만 방법1의 경우 기본적으로 header노드를 가지고 있어 매번 노드의 개수를 고려할 때 1개를 추가적으로 고려해야 하는 부분이 있어 아래 코드들은 방법2를 통해 구현하였다. 실제 개념적인 측면에서의 차이는 없다.
public class Node<T> {
Node<T> left = null;
Node<T> right = null;
T data = null;
}
public class DoublyLinkedList<T> {
private Node<T> head = null;
private Node<T> tail = null;
int length = 0;
~~
이중 연결리스트 추가
이중 연결리스트는 양방향 연결이기에 head 뿐만 아니라 tail 변수도 고려해줘야 하기에 단일 연결리스트에 비해 복잡하다.
따라서 '최초로 Node추가', '맨 앞에 Node추가', '맨 뒤에 Node추가', '중간에 Node추가'로 상황을 4가지로 나누어 구현하였다.
1) 최초로 Node 추가
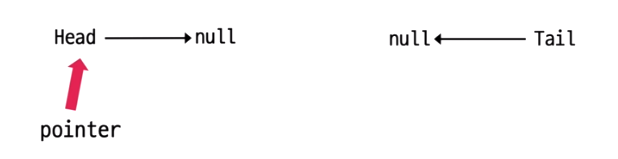
처음 헤드 노드의 모습은 다음과 같다. 데이터를 저장하고 있는 노드가 없고 헤드노드만 존재하기에 head와 tail모두 null을 가리킨다.

최초로 node를 삽입할 때는 헤드 노드의 head와 tail이 모두 새로우 노드를 가리킨다. 최초의 새로운 노드의 left변수와 right변수에는 null을 저장한다. 선행 노드, 후행 노드가 모두 자기 자신인데 가장 첫 번째 노드와 가장 마지막 노드의 주소는 헤드 노드가 저장하고 있기에 별도로 새로운 노드의 left, right변수를 설정할 필요는 없다.
2) 맨 앞에 노드 추가


- 새로운 노드의 right 변수에 헤드 노드의 right변수인 Head 값을 저장한다.
- 새로운 노드의 left 변수에는 null 값을 저장한다.
- 기존 Head가 가리키는 노드(Node A)의 left 변수에 새로운 노드의 주소값을 저장한다.
- 헤드 노드의 head에 새로운 노드의 주소값을 저장한다.
3) 맨 뒤에 노드 추가

- New Node의 left 변수에 헤드 노드의 tail이 가리키는 노드(Node A)의 주소 저장
- New Node의 right 변수에 null 저장
- 기존 tail 노드(Node A)의 right 변수에 새로운 노드 주소값 저장
- 헤드 노드의 Tail변수에 새로우 노드 주소값 저장
4) 중간에 노드 삽입

- New Node의 left 변수에 선행 노드(Node A) 주소값을, New Node의 right 변수에 후행 노드(Node B) 주소값을 저장한다.
- 선행 노드(Node A)의 right 변수에 New Node 주소값을, 후행 노드(Node B)의 left 변수에 New Node 주소값을 저장한다.
public void add(int addIndex, T data) {
Node<T> addNode = new Node<>();
addNode.data = data;
if (this.length == 0) {
//최초 노드 삽입인 경우
this.head = addNode;
this.tail = addNode;
} else if (addIndex == 0) {
//맨 앞에 노드 삽입인 경우
addNode.right = this.head;
this.head.left = addNode;
this.head = addNode;
} else if (addIndex == this.length) {
//맨 뒤에 노드 삽입인 경우
addNode.left = this.tail;
this.tail.right = addNode;
this.tail = addNode;
} else {
//중간에 노드 삽입인 경우
Node<T> rightNode = findNode(addIndex);
Node<T> leftNode = rightNode.left;
addNode.left = leftNode;
addNode.right = rightNode;
leftNode.right = addNode;
rightNode.left = addNode;
}
this.length++;
}
public void addFirst(T data) {
add(0, data);
}
public void addLast(T data) {
add(this.length, data);
}
이중 연결리스트 삭제
1) 노드가 한 개인 경우 삭제할 때
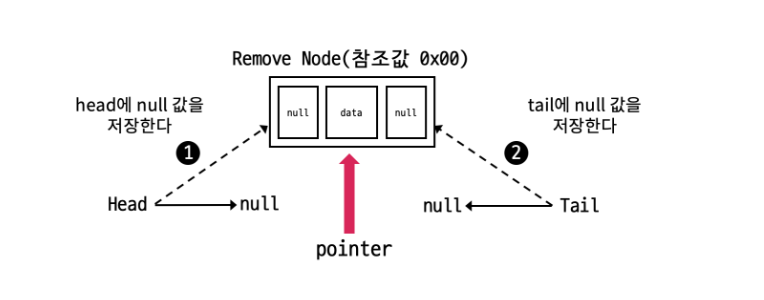
헤드 노드의 head와 tail을 null값으로 바꿔준다. 헤드 노드로부터의 연결이 끊어지면 자동으로 해당 노드를 JAVA의 Garbage Collercor가 해당 노드에 할당된 메모리를 해제한다.
2) 맨 앞 노드를 삭제할 때
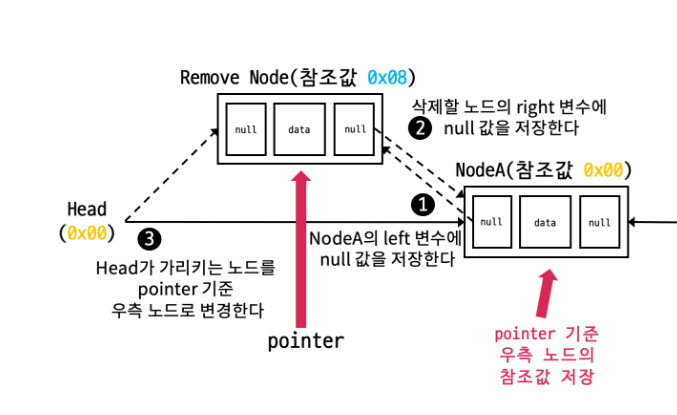
- 삭제할 노드(Remove Node)의 후행 노드(Node A)의 주소를 임시저장한다.
- 삭제할 노드의 후행 노드(Node A)에 있는 left 변수를 null로 변경한다.
- 삭제할 노드의 right변수를 null로 변경한다. (이후 Garbage Collector에 의해 메모리 해제됨)
- 헤드노드의 right변수인 head에 임시저장한 삭제할 노드의 다음 노드(Node A)의 주소값을 저장한다.
3) 맨 뒤의 노드를 살제할 때

- 삭제할 노드의 선행 노드(Node A)의 주소 임시저장한다.
- 삭제할 노드의 선행 노드(Node A)의 right 변수를 null로 변경한다.
- 삭제할 노드의 left를 null로 변경한다. (이후 Garbage Collector에 의해 메모리 해제됨)
- 헤드노드의 left변수인 tail에 임시저장한 삭제할 노드의 선행 노드(Node A)의 주소값을 저장한다.
4) 중간 노드를 삭제

0. 삭제할 노드의 left, right변수에 저장된 선행 노드(Node A)와 후행 노드(Node B)의 주소값을 임시저장한다.
1.2. 선행 노드(Node A)의 right변수에 후행 노드의 주소값을, 후행 노드(Node B)의 left 변수에 선행 노드의 주소값을 저장한다.
3.4. 삭제할 노드의 left, right변수 값을 null로 저장한다. (이후 Garbage Collector에 의해 메모리 해제됨)
public void removeNode(Node<T> removingNode) {
Node<T> leftNode = removingNode.left;
Node<T> rightNode = removingNode.right;
if(isEmpty()){
throw new ArrayIndexOutOfBoundsException();
}
if (this.length == 1) {
//노드가 한 개인 경우
this.head = null;
this.tail = null;
} else if (leftNode == null) {
//맨 앞 노드 삭제인 경우
rightNode.left = null;
this.head = rightNode;
} else if (rightNode == null) {
//맨 뒤 노드 삭제인 경우
leftNode.right = null;
this.tail = leftNode;
} else {
//중간 노드 삭제인 경우
leftNode.right = rightNode;
rightNode.left = leftNode;
}
removingNode.left = null;
removingNode.right = null;
this.length--;
}
public void remove(int removeIndex) {
removeNode(findNode(removeIndex));
}
public void removeFirst() {
remove(0);
}
public void removeLast() {
remove(length - 1);
}
public void removeAll() {
this.head = null;
this.tail = null;
this.length = 0;
}
이중 연결리스트 장점
1. 메모리를 동적으로 할당하여 메모리를 절약할 수 있고 삽입, 삭제가 간단하다.
단일 연결리스트가 배열과 비교했을 때 갖는 장점을 동일하게 갖는다.
2. 단일 연결리스트에 비해 접근이 빠르다.
빅오 표기법으로는 단일 연결리스트와 이중 연결리스트 모두 O(N)이기는 하다. 하지만 이는 최악의 상황을 가정한 것이고 만약 노드가 1,000개인데 900번째 노드에 접근하려고 한다면 이중 연결리스트는 tail에서 부터 접근하여 100번의 이동을,
단일 연결리스트는 900번의 이동을 해야한다.
이중 연결리스트 단점
1. 배열과 비교했을 때 접근이 느리다.
단일 연결리스트에 비해 접근이 빠르지만 배열과 비교했을 때는 여전히 head or tail로 접근을 시작해 순차적으로 접근해야 해서
비교적 속도가 느리다.
2. 단일 연결리스트에 비해 구현이 복잡하다. 별도로 tail 변수가 필요하며 양방향의 연결을 구현해야 하기에
추가, 삭제 연산이 복잡하다.
3. 데이터의 개수가 많아질 수록 접근 연산이 복잡해지고 그에 따라 장접이던 빠른 삽입, 삭제 연산이 느려진다.
시간 복잡도 비교
빅오 표기법으로 나타낸 시간 복잡도는 다음과 같다.
| 이중 연결리스트 | 단일 연결리스트 | 배열 | |
| 접근 | O(N) | O(N) | O(1) |
| 검색 | O(N) | O(N) | O(N) |
| 삽입 | O(1) | O(1) | O(N) |
| 삭제 | O(1) | O(1) | O(N) |
자바에서 배열(array) vs ArrayList vs LinkedList
자바 collections의 LinkedList 순회 시 조심할 점
자바는 별도로 Collections Framework에서 LinkedList를 제공한다.
내부적으로 이중 연결리스트로 구현되어 있으며 원형 리스트의 특징도 추가하여 리스트의 단점인 접근성을 보완하였다.
중요한 점은 자바의 LinkedList에서 get(int index) 메소드를 반복문을 통해 사용해서는 안된다는 점이다.

배열이 그림과 같이 0번째 주소값에서 index크기만큼 더하기 연산으로 접근하기에 접근 연산이 O(1)인 반면
연결리스트는 그림과 같이 노드의 순서에 따라 하나씩 이동을 하여 접근한다.
배열은 크기가 고정되어 값들을 연속적인 주소값으로 저장이 가능하지만 연결 리스트는 크기가 고정되어
있지 않기에 선행 노드와 후행 노드의 주소값이 불연속적이다. 따라서 연결리스트는 배열처럼 단순히
index크기만큼 값을 더하여 접근하는 연산이 불가능하다.
int sum = 0;
for(int i = 0; i < 10000000 ; i++){
sum += linkedList.get(i)
}따라서 위와 같이 반복문을 이용하여 노드에 접근하려는 연산은 시간복잡도 O(n^2)으로 최악의 연산속도를 갖는다.

linkedList.get(0)은 1번
linkedList.get(1)은 2번
linkedList.get(2)은 3번
....
linkedList.get(n)은 n+1번의 접근 연산을 갖기에 O(n^2)의 시간 복잡도를 갖게 된다.
자바에서는 이러한 문제를 Iterator를 사용하여 해결하였다. Iterator는 노드를 순차적으로 이동하며 이전의 접근을 바탕으로 후행 노드의 접근하여 접근 연산이 시간복잡도 O(n)이게 된다. foreach문을 LinkedList로 사용하는 경우 내부적으로 Iterator를 사용한다.
보다 자세한 설명은 아래의 링크를 통해 확인할 수 있다.
[Java] 자바 List 탐색/순회 (for문, 향상된for문, ListIterator)
int sum = 0;
for(Integer value : linkedList){
sum += value;
}
코드 실행
public class Main {
public static void main(String[] args) {
DoublyLinkedList<String> doublyLinkedList = new DoublyLinkedList<>();
doublyLinkedList.addFirst("A");
doublyLinkedList.addLast("B");
doublyLinkedList.addLast("D");
doublyLinkedList.addLast("E");
doublyLinkedList.add(2, "C");
doublyLinkedList.display();
System.out.println("값 C 갖는 노드의 index: " + doublyLinkedList.indexOf("C"));
System.out.println("List는 값 E를 값고 있다: " + doublyLinkedList.contains("E"));
System.out.println("List는 값 F를 값고 있다: " + doublyLinkedList.contains("F"));
doublyLinkedList.remove(1);
doublyLinkedList.display();
doublyLinkedList.removeFirst();
doublyLinkedList.display();
doublyLinkedList.removeLast();
doublyLinkedList.display();
doublyLinkedList.removeAll();
doublyLinkedList.display();
// doublyLinkedList.remove(0);
// Node<String> node = new Node<String>();
// doublyLinkedList.removeNode(node);
//없는 값을 삭제하려고 하기에 ArrayIndexOutOfBoundsException 발생시킴
}
}
- 실행 결과 -

전체 코드
https://github.com/you88311/data-structure/tree/main/doubly-linked-list/src
GitHub - you88311/data-structure
Contribute to you88311/data-structure development by creating an account on GitHub.
github.com
참고
https://www.codelatte.io/courses/java_data_structure
자바 자료구조 강의 - 코드라떼
컴퓨터 공학 2단계 자바 자료구조 강의입니다. 대부분의 프로그래밍하는 과정은 데이터를 다루는 일입니다. 데이터를 어떻게 잘 저장하고 관리할 수 있는지 자료구조에 대해 배웁니다. 자료구
www.codelatte.io
C언어로 쉽게 플어쓴 자료구조 - 천인국, 공용해, 하상호 지음
Java의 정석 3rd Edition - 남궁성 지음
'자료구조' 카테고리의 다른 글
| [자료구조 Java] 이진 탐색 트리(Binary Search Tree) 개념 정리 + 자바로 구현하기 (0) | 2022.07.09 |
|---|---|
| [자료구조 Java] 큐(Queue) 개념 정리 + 자바로 구현하기 (0) | 2022.07.07 |
| [자료구조 Java] 스택(Stack) 개념 정리 + 자바로 구현하기 (0) | 2022.07.02 |
| [자료구조 Java] 단일 연결리스트(Singly Linked List) 개념 정리 + 자바로 구현하기 (0) | 2022.06.30 |
| 자료구조는 왜 알아야 하나? (0) | 2022.06.30 |